The New XOR Problem
In 1969, Marvin Minsky and Seymour Papert published Perceptrons: An Introduction to Computational Geometry. In it, they showed that a single-layer perceptron cannot compute the XOR function. The main argument relies on linear separability: Perceptrons are linear classifiers, which essentially means drawing a line to separate input that would result in 1 versus 0. You can do it in the OR and AND case, but not XOR.
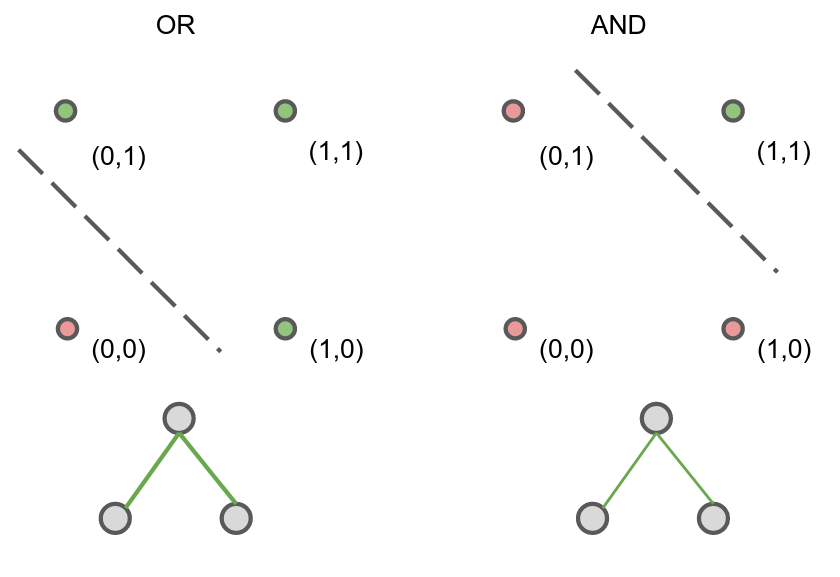
Of course, we’re way past that now, neural networks with one hidden layer can solve that problem.
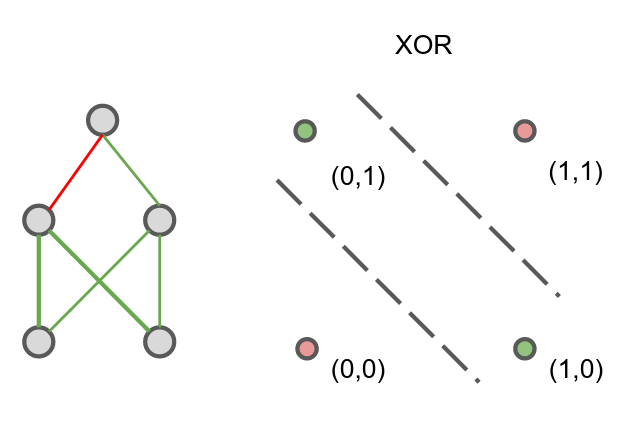
The solution in essence is analogous to composing AND, OR, and NOT gates, which can be represented by single-layer networks, to form the required function.
The key takeaway? Depth is important for certain functions.
Parity
Let’s look at a related but simple problem: Given a binary string, output 1 when there are an even number of 1s in the string, and 0 otherwise. This is often referred to as the PARITY problem (capitalisation because that’s what Theory of Computation people do, not because I’m shouting).
One way to solve it is to chain up a bunch of XOR gates: left XOR input takes the previous XOR output, and right input takes the next bit in the binary string, and then negating the final output. This will give us a circuit that solves PARITY.
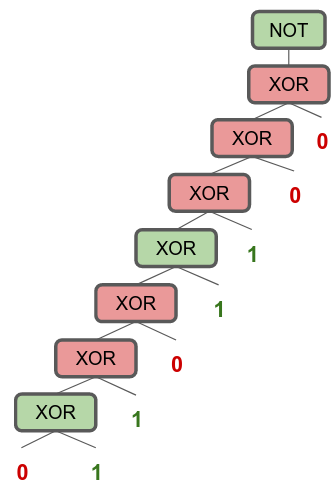
The depth of this circuit grows in $O(N)$.
In sequences with length 2, it’s the complement of the XOR problem: Whatever XOR tells you, flip that bit, and you get PARITY for 2. I’m just going to call this NOT(XOR(.)) gate NXOR.
We can take this property of NXOR and build a magical circuit that grows with the size of the input to solve it. But it grows in a specific way. Divide and conquer helps here: chop the sequence up into pairs of bits, run NXOR on all pairs, take those results, run NXOR on pairs of that output, and so on:
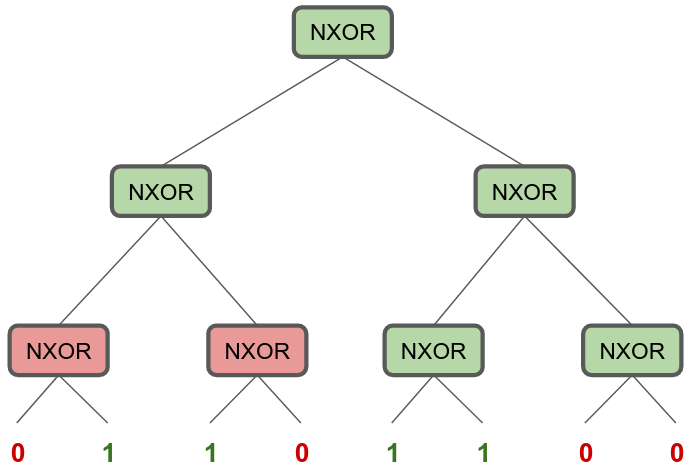
Hopefully at this point, you’re getting traumatic flashbacks to Data Structures 101, and remembering something about complete binary trees and log N depth. And yes, the depth of this circuit to solve parity strings of $N$ length, grows in $O(\log N)$ — The longer the input, the deeper you need to go to solve the problem.
There’s a reason why depth is important here. If you’re designing circuits instead of writing code that executes linearly, computations can be executed in parallel, and the more you can do in parallel, the more time saved. Depth then becomes a convenient analogue to computation time. I’m probably severely oversimplifying because I am severely under-educated in circuit design, but for the sake of where I’m going, let’s pretend I’m right.
We can bring back our neural network that solves XOR, negate the logits at the output (NXOR), and connect them up in a similar way to solve the PARITY problem with neural networks. The network would, like the circuit, grow with the input. The linear-chain version would grow in $O(N)$ and the binary tree version would grow in $O(\log N)$.
In any case, we’d need to get deeper with a bigger input size.
“What would ChatGPT say?": Computational Complexity of Transformers
If you think ChatGPT can solve this, I’ve tried. There has been a recent spate of papers discussing the limitations of a fixed-depth Transformer, which serve as the basis of GPT and friends. Yes, they have a LOT of parameters. Yes, some of them go 96 layers deep. But there are fundamental lower-bound depth complexity issues that make it impossible (for fixed-depth transformers) to generalise to certain types of problems that no amount of parameter scale and data will fix. I will caveat this. Most theoretical findings in deep learning have to make certain assumptions about the premise before anything interesting can be proved. The argument then comes down to whether the assumptions are valid. These results are no exception.
Let’s take a look at the main argument from one of these papers to make things concrete.
In Theoretical Limitations of Self-Attention in Neural Sequence Models by Michael Hahn, Hahn makes a combinatorial argument. The biggest, potentially contentious, assumption he makes is that the attention mechanism is ‘hard’ — only the attended time-step gets the entire weight of the attention, everything else gets a 0, meaning each attention head can only attend to strictly one time-step. Without making further assumptions on the attention or the MLP, we can make a combinatorial argument.
I’m giving my own version of the reasoning Hahn uses, so I’ve simplified a few things to condense everything down. To start with, each Transformer block has $H$ attention heads. In the ‘hard’ attention regime, each of these heads can attend to exactly one other block in the previous layer, and takes the output of the previous layer. And we’ll say that a Trasnformer has $L$ layers.
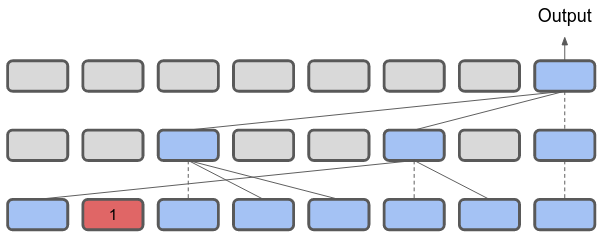
As an example, we have $L = 3$, and $H = 2$.
Tracing from where the prediction is made, say the final timestep, only $H$ other timesteps can be attended to. In turn, each of these $H$ time-steps can attend to $H$ other timesteps, and we can even assume these attended timesteps do not overlap. Given an $L$ layer transformer, we’d, at maximum, be looking at (receptive field in ConvNet speak) $H^L + H + 1$ steps of the sequence. If a sequence is longer than that, some parts of the input would be ignored. PARITY, however, requires taking into account every part of the input sequence — missing a 1 bit in some part of the input would result in the wrong output.
Hard attention is, however, a strong assumption. Saturated Transformers are Constant-Depth Threshold Circuits relax this assumption allowing for saturated attention: Attention weights that are distributed uniformly over $k$ steps. This relaxed assumption boosts the expressibility of Transformers somewhat, but still puts it within the realm of regular languages, or less. The Chomsky Hierarchy is one possible way to categorise computation, but things don’t always map neatly onto it.
Perhaps at this point you’re thinking “So the Transformer isn’t suited for PARITY, you’re testing a fish on how well it would climb a tree. If my grandmother had wheels she would be a bike! Why is PARITY important?” For one thing, it’s one of the simplest formal languages in the set of regular languages. These are languages that can be recognised by a finite state automaton. The one for PARITY looks like this:
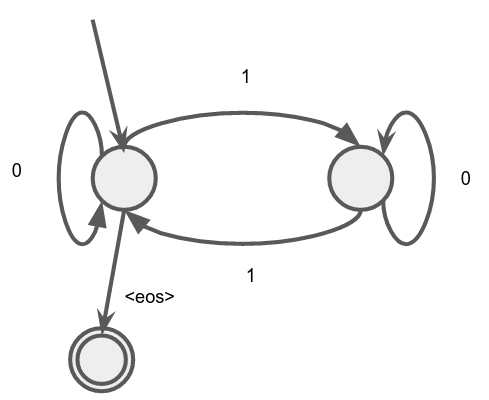
While consuming the string bit by bit, you take the transitions (arrows) associated with the bit. The nodes are the states of the automaton, and only two states need to be tracked: “Are there even or odd bits up till this point in the sequence?”. This is a similar kind of computation as the linear-chain XOR circuit we constructed earlier. There is a formal sub-class of the regular languages that not being able to learn PARITY will exclude, but suffice it to say, if it cannot handle tracking 2 states sequentially, we can start to see other issues that may arise. It’s a sort of canary in the coal mine for even more challenging problems.
To be completely fair, the Transformer architecture does not map neatly into being analysed like automata and categorised in the Chomsky Hierarchy. Neural Networks and the Chomsky Hierarchy train different architectures on formal languages curated from different levels of the Chomky hierarchy. It performs poorly (worse than LSTMs) on PARITY. On the Ability and Limitations of Transformers to Recognize Formal Languages also performed such an empirical study and found similar results.
Overcoming a Theoretical Limitation of Self-Attention deals with the parity problem head-on, adding several elements to the positional embedding and attention system in order to overcome the Transformers’ inability to deal with PARITY. However, the ‘fix’ focuses largely on the PARITY problem, and may not address other issues about the transformers’ expressibility of other regular languages.
Where does this leave us? Given the evidence above, I think we are limited by fix-depth transformers in a severe way. But there are solutions that already exist.
Chain-of-Thought Prompting
This is all the rage in NLP research now, and creeping slowly into the twitterverse: Prompting these LLMs so they “show their work”. It’s exactly what it sounds like, except you’re the teacher now telling the elementary school maths student to write down the exact steps taken to get to their answer.

So far, this technique (and those adjacent to it) have been very successful in raising performance on these in-context learning tasks where the LLMs are not explicitly trained for these tasks, but are given several examples of a problem and a solution as a prompt, and then finally given a problem and expected to generate a solution. In Chain-of-Thought prompting, the solution also involves the intermediate steps taken to give that solution.
Some have seen this as sort of a ‘open sesame’ style magic word to cause the LLM to produce the intended output. I, however, believe for some tasks, it is impossible for a standard Transformer to produce the right answer immediately, and CoT is absolutely necessary. I view CoT as a way for Transformers to maintain state in cases where iterative computation needs to be made. To bring it back to PARITY, the “chain-of-thought” would involve generating also the intermediate states of the above automaton, so it might look something like this:
Q:01101100
A: Even, odd, even, even, odd, even, even, even. The answer is even.
I’ve attempted this prompt several different ways on ChatGPT without a working solution, but I imagine this could work. There has been work that have attempted this for generalisation on the parity problem, but it is by no means ‘solved’.
In terms of where this puts Transformers on the hierarchy though, I think it makes it Turing-complete. A few papers have come out this year that are already exploring what this means for Transformers theoretically. One shows constructions of Transformers doing various tasks by “programming” its weights, and allowing for “external memory” in its output, which can be read in again by another iteration of the same Transformer.
Another shows that, at least for one LLM, the weights of said LLM are able to simulate a Turing machine (thus turing complete) if prompted accordingly, and allowed access to its own output as an external memory. Normally, papers about architecture and computation this ask the question “what is the ‘hardest’ possible thing that this architecture can compute?” (upper bound) whereas in this case, it’s more “Having trained this thing on this data, and ending up with these weights, can it implement a Universal Turing machine?”. It’s entirely possible having been trained on data, the resulting Transformer could simply spout gibberish (Consider a Transformer trained on just strings of 0s). In some ways, the most damning line in the article is in the conclusion:
Success was not achieved with every large language model considered, and effort was required to engineer the prompt.
Since this type of study is empirical, there are a whole slew of reasons this could happen. Prompting to be a Universal Turing machine isn’t exactly the data these models look at during training, so it kinda should be expected? Or, perhaps the author just didn’t find the right prompt for it for these other models? Concluding that these other models, with prompting, are not Turing complete is just one of the many conclusions one could arrive at. This uncertainty cuts both ways: Just as we are uncertain about the failures of these models, we should be uncertain about the capabilities they have appeared to have demonstrated so far.
Returning to prompting: This technique is only employable in cases where we already know the way to solve the problem in question, which is the only way you’d be able to create such a prompt to guide the model’s generated solution. This is assuming that our techniques at prompt engineering get better over time, which I think it will. It is, still, very much an art, one that I find myself sorely lacking talent in, given my attempts at prompting for PARITY. Periods, spaces, question marks, where you put them matters. Prompt engineering is the new feature engineering, at least for now.
Universal Transformers
Universal Transformers are Transformers for which all parameters are shared across all layers. There is also an added halting mechanism that decides for each timestep when to stop updating. Everything else works like a standard Transformer: Get the input sequence, extract the embeddings for each token, apply the first layer of the Transformer transformation, the second, and so on. In the idealised Universal Transformer, since all layers of transformers are equal, the same layer can be applied indefinitely until the halting mechanism signals halt for all timesteps. This version of the Universal Transformer is Turing complete.
It is not obvious how many iterations of UT needs to be applied before computation can be terminated. Consider how we figured out the depth required for PARITY; not all problems have a similarly analysable structure. This poses a problem during training – a maximum depth needs to be set, or, the depth of the UT is determined by a function of the size of the input. On the PARITY problem, we can make this log n, or n, if the input is of length $N$.
I trained a UT on PARITY that runs the UT transformation $N$ times for an input of length $N$. Training only for length 1 to 40, and I tested it on lengths 1 to 300. This is the resulting plot, against a vanilla Transformer:
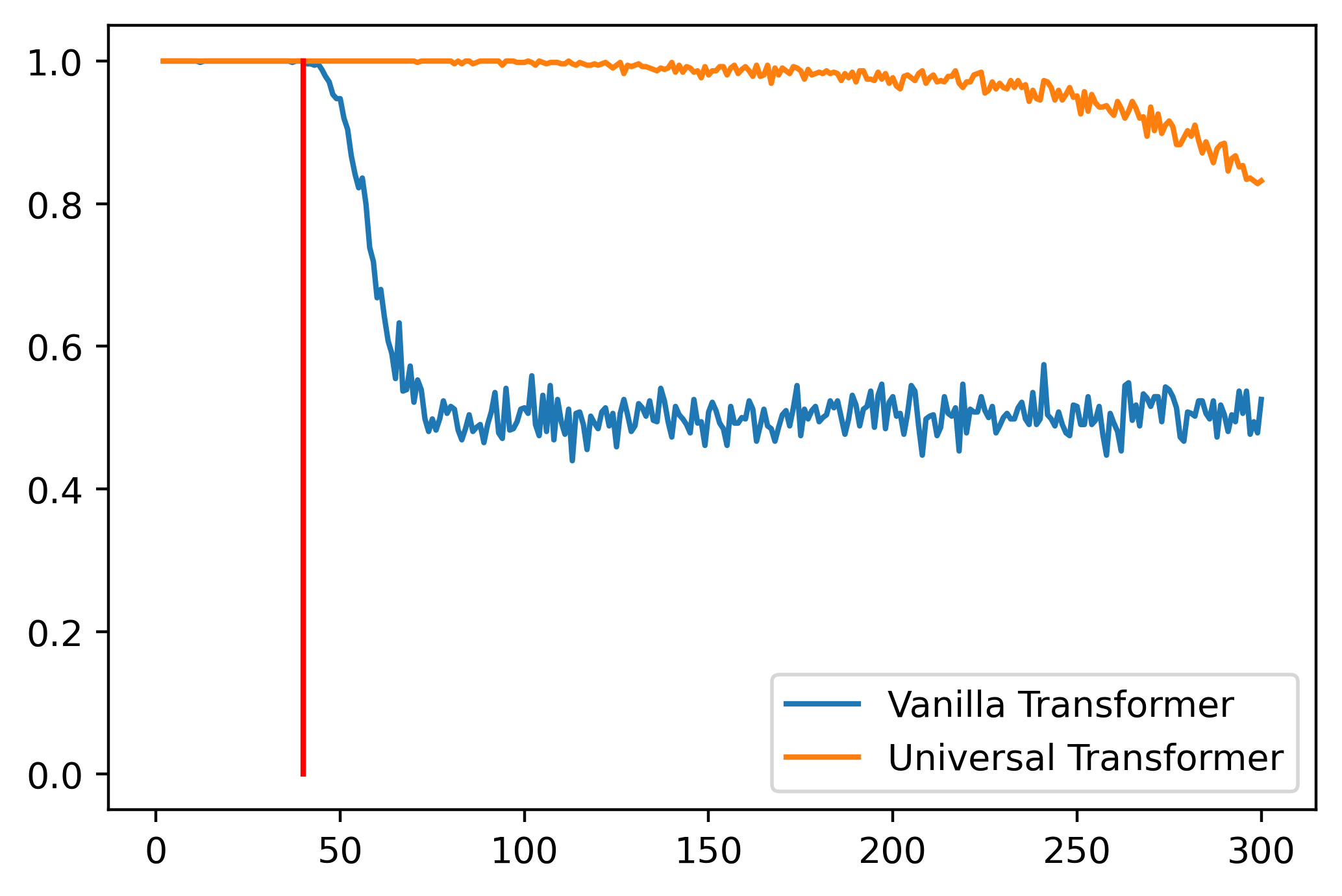
It generalises somewhat, better than the vanilla Transformer at the very least. But we paid for it in computation time. The whole reason for choosing Transformers over the RNN models was that it was far more parallelisable during training — the depth of the Transformer was independent of the input, which meant evaluating a Transformer on a {T,G}PU was extremely parallelisable, nearly constant. An RNN, however, had to have each hidden state computed one after another, making it much slower in comparison. Using a UT like this would mean a return to RNN-like sequential computation.
Of course, one could assume a maximum depth for the problem and hope for the best, which I think is a reasonable way forward. UTs have a lot of potential and it’s strange to me why they aren’t more widely adopted. If I were to guess, I think there are issues of computation costs in scaling up UTs.
These two paths come with their own issues, but I only suggest these as they seem the most likely. There are other esoteric architectures out there that are less efficient (in terms of compute) that may ‘scale’ the Chomsky hierarchy more obviously, but are a nightmare to get working on actual data, if it ever works at all.
Ostrich
Or you know, if we deal only in language, perhaps none of that needs to matter at all. Hao et. al. opine in their conclusion:
Finally, given the success that Transformers have had as models of natural language, it is perhaps surprising that these models’ expressive power seems to be best characterized (or at least bounded) in terms of circuit complexity. Mathematical explorations of natural language have most commonly employed the approach to language complexity afforded by the Chomsky hierarchy and its refinements, which is based on automata and formal grammars. The apparent incomparability of these approaches suggests that the exploration of different types of Transformer models might offer a new approach to the study of the formal properties of natural language.
Translated from academese: “Maybe human language is simpler than we thought, and doesn’t require higher levels of the Chomsky hierarchy… We might be Transformers!”. (Yes, I know, it’s not quite that) I don’t believe it, but I do think one way I can be wrong is in this way.
XOR and its legacy
Minsky and Papert’s book and the limitations of the perceptron have often been cited as a contributing factor for the first AI winter. While I think things must’ve already been mighty frosty at the time for this one simple problem to induce a snowstorm, I highly doubt people weren’t talking about possible solutions. According to the answers here, Rosenblatt knew MLPs would fix things, and to some extent, Minsky and Papert probably knew as well. How MLPs could be trained was an open problem at the time, I think, but the field could easily have chugged along and we’d have been where we are now, just 30 years earlier. A large issue was in not managing expectations when it came to AI, and we’ve had 2 cycles to learn that hype trains can maglev themselves into a 10-year ditch. Think clearly about limitations, and communicate them clearly.
All this to say: I think there are fundamentals we need to view all of this progress through. Lower-bound complexities of problems that we learn in Algorithms 101 shouldn’t get thrown out the window because linear algebra, ReLUs and attention mechanisms are involved. Sorting, for example, has a provable lower-bound complexity of $\Omega(N \log N)$. When someone tells you there is a way to do it in $O(\log N)$ time, it’s best to squint and ask a few questions. When someone tells you you can gain a speed-up in computing primes, on a naive algorithm, it’s best to ask if that method also has correctness covered.
I do think we’re still in good shape, but the discourse is getting ridiculous.
@misc{tan2023-02-03,
title = {The New XOR Problem},
author = {Tan, Shawn},
howpublished = {\url{https://blog.wtf.sg/posts/2023-02-03-the-new-xor-problem/}},
year = {2023}
}